最强尺规作图，仅用直尺和圆规画出一颗完美的鸡蛋

尺规作图指用无刻度的直尺和圆规作图，是数学分支几何学中很重要的一个课题。在中国的教育当中，一般到初中才会系统地教一些尺规作图的知识技巧，但是画出来的图形一般也仅限于一些简单的圆弧或者切线什么的，这些圆弧或者切线什么的一般都难以组合成比较复杂优美的图形，更别说是有意义的图形了。

如果我说利用尺规作图，可以画出鸡蛋，你信吗？在看过这篇文章的介绍之前，我相信很多人应该是不信的。可是，这世界还真的有人利用尺规作图画出了一颗完美的鸡蛋。之所以说完美，只是因为你可以对照现实当中的鸡蛋，你会发现现实当中几乎没有鸡蛋的比例能像这个鸡蛋图形一般线条完美，比例均匀。

欧氏蛋的画法是由一名叫做罗伯特·坦肯的人创造出来的。之所以叫做欧氏蛋，是因为这个蛋的画法属于欧几里德几何学的范畴。

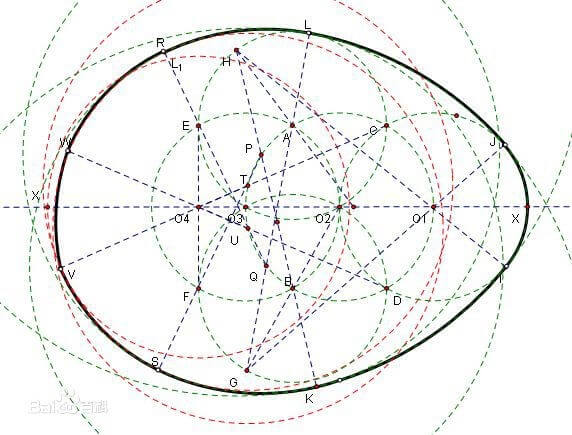
欧式蛋图形如下：

作图步骤：

1 在MN上任取一点O1为圆心，以任意长为半径画圆O1与MN交于O2和X。

2 以O2为圆心，O1O2长为半径画圆O2，与MN交于O3.

3 以O3为圆心，O2O3长为半径画圆O3与圆O2交于AB。

4 以A为圆心，O2A为半径，画圆A，与圆O1O3分别交于CE。

5 以B为圆心，O2B为半径，画圆B交圆O1O3分别于DF。

6 连结O2B，并延长交圆B于G。

7 连结O2A，并延长交圆A于H。

8 连结HO1并延长交圆O1于I。

9 连结GO1并延长交圆O1于J。

10 连结HB并延长。

11 连结GA并延长。

12 以H点为圆心，HI为半径画弧IK,与HB延长线交于K。

13 以G为圆心，GJ为半径画弧JL，交GA延长线于L。

14 线段HB与圆O2交于P，连结PF并延长。

15 线段GA与圆O2交于Q，连结QE并延长。

16 以P为圆心，PK为半径画弧KS，与PF延长线交于S.

17 以Q为圆心，QL为半径画弧LR，交QE延长线于R

18 连结EF与MN交于O4

19连结CO4与圆O2交于T。

20连结DO4与圆O2交于U。

21连结TO4并延长

22 连结UO4并延长

23 以T为圆心，TS为半径画弧SV，交TO4延长线于V。

24以U为圆心，UR为半径画弧RW，交VO4延长线于W。

25以O4为圆心，O4V或O4W为半径画弧VW，与MN交于Y。

由以上弧XJ,JL,LR,RW,WY,YV,VS,SK,KI,IX十段弧线连成的曲线即为一个蛋。

根据以上描述，我们可以知道欧氏蛋虽然造型优美，但是缺点在于步骤繁多，其实鸡蛋还有另外一种相对简单的画法，只需要8步即可完成，这种鸡蛋的画法由英国考古学家亚历山大·汤姆创造，所以叫做汤比蛋。不过，汤比蛋在外形上相对简单，也没有欧氏蛋那么优美。

汤比蛋图形如下：

作图步骤：

1.画直线XY与MN垂直，并相交于O点。

2.以O为圆心，以任意长为半径画一个圆，该圆与MN相交于A,B，与XY相交于C。

3.以C点为圆心，以CA或CB长为半径画圆弧⌒AHB，并与XY相交于H。

4.连A,C并延长与圆弧⌒AHB相交于D。

5.连B,C并延长与圆弧⌒AHB相交于E。

6.以A为圆心，AD之长为半径画圆弧⌒DF，它与MN相交于F。

7.以B为圆心，BE之长为半径画圆弧⌒EG，它与MN相交于G。

8.以O为圆心，OG或OF之长为半径画半圆⌒GIF，并与XY相交于I。

曲⌒EHD，⌒DF，⌒GIF，⌒EG相连的由基即为一个汤比蛋。